Отрадно и то, что уровень работ оказался высоким. Это говорит о сохранении интереса к астрономии у школьников даже в нынешние не самые легкие времена. Задачи были достаточно сложные, и тем не менее многие работы были оценены очень высоко.
Как и в прошлом году, решение каждой задачи оценивалось по пятибалльной системе, тем самым максимальное количество баллов равнялось 30. К сожалению, в отличие от прошлого года, никому не удалось взять эту "наивысшую планку". Однако нескольким участникам удалось подойти к ней достаточно близко. Победителем Второй Открытой российской заочной школьной астрономической олимпиады с результатом 27 баллов стал ученик 11 класса лицея № 1 г. Тулы Дмитрий Куланин. Вторая по силе работа пришла от ученика 11 класса школы №1543 г. Москвы Артема Аэрова. Он уступил победителю всего одно очко и набрал 26 баллов. Еще на балл меньше (25 баллов) набрали сразу два участника олимпиады, поделившие третье место. Это победитель прошлогодней олимпиады ученик 10 класса школы №518 г Санкт-Петербурга Дмитрий Бакай и 11-класс-ник из школы №1103 г. Москвы Николай Подорваток.
Семь участников олимпиады стали дипломантами. Это Павел Семеюота (9 класс, г. Прохладный), Кирилл Соколовский (8 класс, г. Москва), Алексей Тягунов (10 класс, г. Москва), набравшие по 23 балла, Светлана Игошина (11 класс, г. Стерлитамак), Дмитрий Старицын (9 класс, г. Архангельск), набравшие по 22 балла, Игорь Екимов (9 класс, г. Лесной) и Юрий Каратассо (11 класс, г. Москва), набравшие по 21 баллу.
Самой сложной на олимпиаде оказалась последняя, шестая задача. Никому из одиннадцати призеров и дипломантов не удалось решить ее полностью. И лишь один участник олимпиады, Ильгиз Хазнев, ученик 9 класса школы №2 г. Прохладный Кабардино-Балкарской республики, сумел дать исчерпывающее решение этой задачи. Поэтому жюри приняло решение наградить его специальным призом олимпиады.
Мы поздравляем всех отличившихся участников олимпиады с успешным решением задач. Им будут высланы дипломы, а призерам — также ценные призы.
Ответы на вопросы
1. Космический корабль будущего стартует с Земли в направлении северного Полюса мира, постепенно увеличивая свою скорость до околосветовой. Опишите характерные изменения в виде звездного неба, которые заметят его пассажиры
Основные эффекты, которые будут сказываться при разгоне космического корабля до околосветовой скорости — это эффект Доплера и аберрация света. Первый из этих эффектов приведет к смещению спектров звезд по курсу корабля в фиолетовую сторону, а звезд, оставшихся позади — в красную. В результате звезды в северном полушарии неба станут "голубеть", а в южном — "краснеть". Одновременно с этим в северном полушарии неба появятся новые красные звезды, излучающие в основном в инфракрасной области спектра и поэтому невидимые с Земли, в южном полушарии станут видимыми ультрафиолетовые источники излучения. При скорости, близкой к скорости света, мы уже не сможем видеть обычные звезды вблизи полюсов, зато станут видны радиоисточники около северного полюса мира и рентгеновские и гамма-источники — около южного полюса. Также начнет сказываться и поперечный эффект Доплера: в красную сторону станут смещаться спектры звезд вблизи экватора, сбоку по курсу корабля. Аберрация света приведет к смещению положения звезд в сторону северного Полюса мира, и особенно сильно она будет сказываться вблизи экватора.
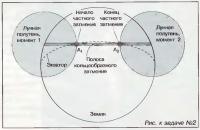
2. В некоторой точке Земли наблюдается солнечное затмение с максимально возможной общей продолжительностью (от первого до последнего касания дисков Солнца и Луны). Какого типа это затмение (полное, кольцеобразное, частное) и почему?
Если предположить, что это затмение было центральным (простой вариант решения), то на продолжительности будут сказываться расстояние, которое должен пройти диск Луны относительно диска Солнца и скорость его движения. Расстояние, очевидно, тем больше, чем больше угловые диаметры Солнца и Луны но гораздо сильнее на картину влияет скорость диска Луны, которая минимальна, когда Луна находится в апогее, т.е. когда ее размер минимален. В этом случае расстояние уменьшается, но незначительно (на него влияет еще и размер Солнца), а угловая скорость, как можно убедиться из II закона Кеплера, убывает намного сильнее.
В результате максимальная продолжительность затмения будет при максимальном угловом размере Солнца и минимальном угловом размере Луны, то есть это затмение будет кольцеобразным. Эффект скорости вращения Земли увеличивает продолжительность любого затмения, не изменяя баланс между продолжительностью полного и кольцеобразного затмения.
Однако если решать задачу более точно, то необходимо учесть, что путь диска Луны относительно диска Солнца в результате вращения Земли вокруг своей оси не будет прямолинейным, и затмение не должно быть центральным. На это обратил внимание только один участник олимпиады. Действительно, самое длительное затмение должно наблюдаться в экваториальной зоне Земли около зимнего солнцестояния, когда диск Солнца имеет максимальные размеры, а скорости движения лунной тени и полутени и вращения поверхности Земли направлены в одну сторону. Но при этом путь земного наблюдателя не будет прямым, и он увидит частное, хотя и очень близкое к кольцеобразному, затмение Солнца.
3. Спутник Юпитера Ио находится между Солнцем и Юпитером. Во сколько раз его дневное полушарие освещено сильнее, чем ночное?
Эту задачу можно решать различными путями. Самый простой на наш взгляд вариант следующий. Очевидно, что дневную сторону Ио освещает Солнце, а ночную — полный Юпитер (см. рис. вверху). Зная звездные величины Солнца (-26.8m) и Юпитера (например, в противостоянии 1998 года — -2.9m) при наблюдении с Земли и расстояния от Солнца до Земли, от Солнца до Юпитера и Ио в 1998 году и от Юпитера до Ио, мы вычисляем звездные их величины при наблюдении с Ио. Мы получаем m☉=-23.2m и m2=-18.6m, откуда следует, что дневное полушарие Ио будет освещено приблизительно в 70 раз сильнее, чем ночное.
4. Какую из двух звезд: Альтаир (α Орла) или Процион (α Малого Пса) можно непрерывно наблюдать на темном небе в течение большего промежутка времени на широте Москвы? Какую из этих звезд можно дольше наблюдать на темном небе ежедневно в течение года на той же широте?
Эти звезды имеют близкие значения склонения, чуть большие нуля. Обе звезды находятся над горизонтом на широте Москвы около 13 часов каждые сутки. Но они находятся в противоположных областях неба, и условия их наблюдения оказываются совершенно разными. Процион — "зимняя звезда", и длинными зимними ночами ее можно наблюдать все 13 часов от восхода до захода. Весной Процион виден вечером, осенью — утром, а летом не виден вообще.
Альтаир же — "летняя звезда", и лучше всего она видна летом, но продолжительность ее видимости ограничена короткими летними ночами. Осенью Альтаир виден вечером, весной — утром. Но Альтаир виден и зимой, заходя за горизонт уже после начала длинной зимней ночи, и восходя еще до ее окончания.
Ответ задачи следующий: непрерывно наблюдать на темном небе дольше можно Процион, так как он виден в январе с восхода до захода. Но Альтаир можно наблюдать ежедневно в течение всего года (если бы, конечно, позволяла погода), а Процион пропадает с неба на широте Москвы практически на все лето.
5. Почему солнечные затмения могут происходить в любой сезон года, а прохождения Венеры по диску Солнца — только в начале июня и начале декабря?
Известно, что как орбита Луны вокруг Земли, так и орбита Венеры вокруг Солнца наклонены к плоскости эклиптики на некоторый угол. Поэтому далеко не в каждое новолуние происходит солнечное затмение и не в каждое нижнее соединение Венеры — ее прохождение по диску Солнца. Для наступления такого явления еще нужно, чтобы Луна или Венера находились вблизи одного из узлов своих орбит — точек их пересечения с плоскостью эклиптики.
Но положения узлов орбиты Венеры практически не изменяется со временем, и они соответствуют положению Земли в начале июня и начале декабря — именно тогда возможно наступление такого редкого астрономического явления, как прохождение Венеры по диску Солнца. Узлы же орбиты Луны вращаются с периодом чуть больше 18 лет, и поэтому в разное время солнечные затмения могут происходить в любой сезон года.
6. Некая обитаемая планета имеет два естественных спутника. Какие из вышеприведенных конфигураций (рис. вверху) этих спутников могут наблюдаться на небе этой планеты, а какие — нет?
Эта задача оказалась самой сложной. Очень немногим удалось найти ключ к ее разгадке, и только одному участнику удалось дать совершенно правильный ответ.
В условии задачи ничего не сказано о форме орбит и размерах спутников, так что заранее неизвестно, какой из них находится ближе к наблюдателю в той или иной конфигурации. Очевидно, что правый спутник в фазе тонкого серпа должен располагаться на небе неподалеку от центральной звезды и не может быть рядом с полностью освещенным левым спутником. Но правый спутник может находиться в тени другого тела! Заметим, что на всех четырех рисунках терминатор правого спутника проходит через его полюса, но имеет форму дуги окружности, а не полуэллипса!
В этом случае возможными становятся варианты а) и в) если предположить, что правый спутник находится в тени планеты. Однако такая ситуация невозможна в конфигурациях б) и г) — в этом случае тень планеты неминуемо попала бы и на левый спутник. Но в случае г) правый спутник может находиться в тени левого! Очевидно, что при этом левый спутник находится не точно противоположно звезде, но он может быть очень близко от точки "противозвезды" на небе, и отличие его фазы от полной будет совершенно незаметным.
А вот конфигурация б) невозможна и в этом случае, так как при этом тень от левого спутника имела бы больший угловой диаметр, чем сам спутник. Этого, разумеется, не может быть. Итак, на небе этой планеты два спутника могут находиться в конфигурациях а), в) и г) и не могут быть в конфигурации б).