Три раза "да!" — вот ответы на эти вопросы! Олимпиада превзошла все наши ожидания, и эксперимент можно назвать удавшимся. В соревнованиях приняли участие 58 человек из 25 городов России, Украины и Белоруссии. И что самое приятное — несмотря на то, что некоторые из задач казались нам весьма сложными для школьников, уровень присланных работ оказался очень высоким. Большое количество участников справилось со всеми или почти со всеми заданиями, и теперь тяжелая задача встала уже перед членами жюри.
Решение каждой из 6 задач оценивалось по пятибалльной системе, тем самым максимально возможное количество баллов было равно 30. И эта "вершина" была покорена одним из участников! Абсолютным победителем Открытой российской заочной школьной астрономической олимпиады 1997 года с наивысшим результатом в 30 баллов стал ученик 9 класса 518 школы г. Санкт-Петербурга Дмитрий Бакай. Второе место занял ученик 11 класса 123 школы г. Москвы Вячеслав Журавлев (27 баллов), третье — 10-классник Педагогического Лицея г. Калининграда Антон Задорин (26 баллов).
Кроме трех призеров, еще девять участников олимпиады стали дипломантами. В их числе: Воронин Петр (11 класс, г. Волгоград), Лемешев Виктор (10 класс, г. Тихвин), Степовик Алексей (8 класс, г. Саратов) и Усанин Владимир (6 класс, г. Казань), набравшие по 24 балла, а также Барташевич Алексей (10 класс, Нижний Новгород), Голубинский Юрий (11 класс, Симферополь), Петрова Ольга, Сиротин Сергей и Шпашная Вероника (все — 11 класс, г. Нижний Новгород), набравшие по 23 балла.
Редакция журнала Звездочет от всей души поздравляет всех призеров и дипломантов с успешным выступлением на олимпиаде. Всем отличившимся будут высланы соответствующие дипломы, а призерам олимпиады — еще и ценные подарки.
В заключение хотелось бы выразить искреннюю благодарность всем участникам олимпиады и всем, кто помог ее организовать. Хочется надеяться, что Открытая российская заочная школьная астрономическая олимпиада станет ежегодной традицией, и что год от года количество ее участников будет только увеличиваться!
Решение задач
1. На Земле произошло полное солнечное затмение. Его полная фаза наблюдалась в северном полушарии и во всей полосе была видна очень низко над горизонтом сразу после восхода Солнца. В какой сезон года это могло произойти?
Вначале определим, в каком случае может произойти полное солнечное затмение, всюду видимое низко над горизонтом. Очевидно, что при этом конус лунной тени должен только задеть Землю, не отходя далеко от ее лимба. При этом в нашем случае он должен задеть Землю с северной стороны.
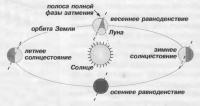
Далее обратимся к рисунку, на котором показана орбита Земли вокруг Солнца и положение ее оси вращения во время солнцестояний и равноденствий.
Ввиду того, что лунная орбита наклонена к плоскости эклиптики на небольшой угол (около 5°), путь лунной тени по Земле будет также практически параллелен плоскости эклиптики. Из рисунка прекрасно видно, что из четырех положений Земли лишь во время весеннего равноденствия тень, задевая Землю с севера, может все время оставаться у ее лимба левее полуденной линии, то есть там, где Солнце только взошло над горизонтом.
Полный же ответ такой: подобное затмение возможно в течение полугода, между зимним и летним солнцестоянием, максимальная же вероятность его наступления — вблизи весеннего равноденствия.
2. Какое максимальное количество планет ярче От можно одновременно наблюдать в одном созвездии ? На всем небе ?
Перечислим для начала все планеты, блеск которых может хотя бы иногда превышать 0т. Это Меркурий, Венера, Марс, Юпитер и Сатурн. Последняя из этих планет может иметь отрицательную звездную величину в противостоянии вблизи перигелия своей орбиты только тогда, когда ее кольца раскрыты. Такая ситуация сложится во время нескольких противостояний Сатурна, начиная с 1999 года. В принципе, все пять планет при этом могут одновременно находиться над горизонтом (например, вечером: Меркурий и Венера на западе, а Марс, Юпитер и Сатурн, находясь вблизи противостояния, восходят на востоке). Чтобы ответить на вопрос, сколько планет с блеском ярче 0т можно увидеть в одном созвездии, учтем, что Меркурий и Венера далеко от Солнца на небе не отходят, и Марс с Сатурном, находясь рядом с ними, столь яркими быть не могут. Поэтому в одном созвездии могут быть только три яркие планеты: либо Меркурий, Венера и Юпитер, либо Марс, Юпитер и Сатурн.
3. На какое полушарие Луны — видимое или невидимое — падает в среднем больше солнечного света и почему?
Эта задача оказалась самой сложной на олимпиаде, и лишь победителю удалось справиться с ней полностью. Для ее решения необходимо учесть четыре фактора, приводящие к неравномерности распределения солнечной энергии по двум полушариям Луны, и сравнить их.
Первый фактор, играющий в пользу обратного полушария Луны, состоит в том, что когда на обратном полушарии Луны день (в новолуние), наш спутник находится ближе к Солнцу, чем когда день на видимом полушарии (в полнолуние). Приблизительная оценка приводит к тому, что этот фактор дает выигрыш около 1% в пользу обратного полушария Луны.
Кроме этого, на обратной стороне Луны не бывает солнечных затмений, "отнимающих" солнечную энергию у видимого полушария Луны. Выигрыш от этого фактора составляет примерно 0.03% (его можно оценить, исходя из частоты теневых лунных затмений на Земле).
Но есть еще два фактора, играющих в пользу видимого полушария Луны. Первый из них состоит в том, что из-за конечности расстояния до Солнца день на видимом полушарии Луны чуть длиннее. Выигрыш в пользу видимого полушария Земли чуть больше 0.3%.
И последний фактор — видимое полушарие Луны, в отличие от обратного, получает солнечный свет не только от Солнца, но и от Земли. Однако, зная яркость Земли на Луне, нетрудно убедиться, что выигрыш видимого полушария Луны не превышает 0.01%.
Сравнивая эти оценки, мы приходим к выводу, что больше солнечного света получает обратное полушарие Луны, хотя разница составляет менее одного процента.
4. Можно ли, проводя наблюдения одним глазом, закрыть спичкой звезду на темном ночном небе?
То, что угловой диаметр спички больше углового диаметра звезды, очевидно. Но не стоит забывать, что в темноте диаметр человеческого зрачка расширяется до 6 мм и более, значительно превышая диаметр спички. Таким образом, независимо от расстояния от глаза до спички, звезду закрыть не удастся. Она лишь немного ослабнет. Некоторые из участников олимпиады даже провели соответствующий эксперимент и удостоверились, что звезда остается видимой.
5. Звезда имеет блеск 0m и координаты α=18h, δ=—23°. Удастся ли ее хоть раз в году увидеть невооруженным глазом на северном полярном круге?
Широта северного полярного круга равна φ=66.5°. Указанная звезда на этой широте будет восходить очень ненадолго, поднимаясь в верхней кульминации на высоту 1° (с учетом рефракции). Но в этот момент (звездное время 18Ч) на северном полярном круге эклиптика совпадает с горизонтом. То есть, когда звезда поднимается над горизонтом, Солнце находится либо низко над горизонтом, либо очень неглубоко под ним. Увидеть звезду 0m ниже 1° над горизонтом в таких условиях, естественно, не удастся независимо от времени года.
6. "Солнце уже зашло, и узенький серпик Луны был прекрасно виден. Петя не отрывал глаз от окуляра, боясь пропустить красивейшее явление. И вдруг на краю лунного диска вспыхивают сразу две яркие точки, как будто это была двойная звезда, состоящая из очень ярких компонент, разделенных промежутком чуть меньше одной угловой минуты. И лишь затем точки превратились в дужки и, наконец, соединились друг с другом. Рядом с Луной теперь светила Венера, также имеющая вид тонкого серпа. Хоть она и была намного меньше, но светила чуть ли не ярче всей Луны". Допустил ли автор ошибку в описании астрономического явления ?
Ошибка в описании астрономического явления есть. Очевидно, что в момент покрытия серпики Луны и Венеры должны быть направлены в одну сторону. Покрытие происходило вечером, значит Луна была молодой и двигалась относительно Венеры рогами вперед. Тогда при открытии сначала должен был выйти освещенный лимб Венеры, а лишь затем рога. Описанное же явление могло произойти утром перед восходом Солнца при покрытии Венеры "старой" Луной.
Других ошибок автором допущено не было. Угловой диаметр Венеры в фазе тонкого серпа действительно может быть равен одной угловой минуте. При этом ее яркость может не уступать яркости тонкого серпа Луны, а в телескоп на сумеречном небе маленькая Венера может показаться намного ярче Луны.